 (1)
(1)
LAB 3 - Minor Losses in Pipe Flow
Introduction
For flow in a circular pipe, an expression for the head loss due to skin friction can be developed by applying the principles of conservation of energy and linear momentum [1]. The expression that results for pipe-head loss hf is
 (1)
(1)
where: f = Darcy friction factor
V = average
flow velocity
L = pipe length
g = acceleration due to gravity
d = pipe inside diameter
Equation 1, known as the Darcy-Weisbach equation, is valid for duct flows of any cross section and for either laminar or turbulent flow. The Darcy friction factor is a function of both the Reynolds number and the pipe relative roughness
 (2)
(2)
where Red = Reynolds number based on inside diameter
e = absolute roughness
tw = shear stress at the pipe wall
r = fluid density
Whereas the Darcy-Weisbach equation is valid for both flow regimes, the form of the functional relationship for the friction factor is dependent on the type of flow. For laminar flow, the exact theory for the friction factor results in an expression which is independent of relative roughness,
 (3)
(3)
For fully turbulent flow, an adequate expression for friction factor is more difficult to determine from theory. An accepted practice is to determine the friction factor from the Moody chart for pipe friction. The Moody chart was developed from the Colebrook equation [2], an interpolation formula based on experimental data. While the Colebrook equation was used to develop the Moody chart, it is cumbersome to use. An alternate explicit formula attributed to Haaland [3] is
 (4)
(4)
In addition to skin friction losses in pipe flow, there are additional minor losses due to fittings, valves, gradual and sudden expansions or contractions, and entrance and exit effects. Since the flow patterns in valves and fittings is quite complex and varies from one manufacturer to another, there is no accepted theoretical means of determining these minor losses. The losses are usually measured experimentally and correlated with the pipe flow parameters (Red, e/d). The measured minor loss is typically expressed as a ratio of the head loss hm = Dp/rg through the fitting or valve to the velocity head V2/2g of the attached piping system. The resulting ratio is called the loss coefficient K for the fitting or valve
 (5)
(5)
Thus, the minor losses may also be expressed in terms of the velocity head once the loss coefficient has been determined
![]() (6)
(6)
An alternate method for reporting minor losses is to calculate an equivalent length, Leq, of pipe that produces the same head loss as the fitting. This equivalent length may be determined by equating the Darcy-Weisbach equation (eqtn. 1) to the minor losses equation (eqtn. 6) and solving for Leq. This yields Leq = Kd/f.
Objectives
The objective of this exercise is to determine the minor loss coefficients and associated loss in head for a variety of pipe fittings.
Apparatus
The Cussons Hydraulic Bench consists of a steel frame carrying equipment upon two platforms and an instrument panel. At the lower level is the water reservoir and circulating pump; at the upper level, the frame forms a cradle for the drainage tray/working surface. A bucket for measuring water flow is suspended below the drainage tray. The instrument panel includes a pressure gage and pump control valve. The hydraulic bench is shown schematically in Figure 1.
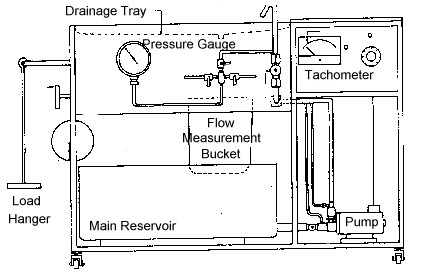
Water is drawn from the main reservoir by the centrifugal pump and delivered via a plastic flexible hose to the control valve mounted on the front panel. From this point the water is delivered to the test panel using another section of flexible hose. After use, the water is discharged into the drainage tray, passing into the bucket of the measuring apparatus which is carried on a beam. The free end of the beam is designed for use with a hanger carrying masses of a known value. Flow rates can be measured by timing the accumulation of water in the bucket with a stop watch. The measurement bucket is emptied using a drain plug at its base. When measurement of the water flow rate is complete, the water is emptied back into the main reservoir.
The pump is a high speed centrifugal type. The motor normally operates at 5000 rpm with a maximum flow rate of 45 liters/min. The maximum head produced is 14 m. A controller is connected to the motor which allows the speed to vary between 0 and 5000 rpm. Speed is indicated by means of an analog tachometer.
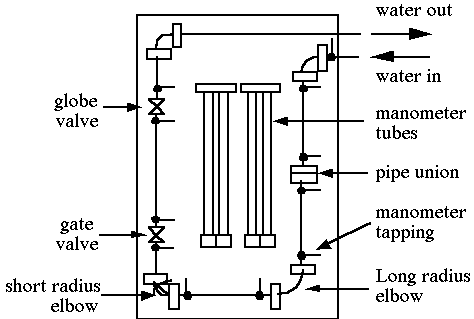
The Pipe Bends and Fitting Apparatus enables friction losses in various types of pipe fittings to be determined experimentally. The apparatus consists of a test length of pipe work (pipe i.d. = 0.794 in) fitted to a vertical panel. The fittings include a pipe union, globe valve, gate valve and pipe bends of different forms. Immediately before and after each fitting are manometer tappings fitted with stopcocks. Mounted into the center of the panel are 4 manometer tubes which can be connected by means of flexible rubber tubes to the manometer tappings on either side of the fitting being tested. The difference in manometer heights will indicate the loss in head caused by the fitting. The test apparatus is shown schematically in Figure 2.
Flow Rate Measurement
The water discharged from the test apparatus falls into the drainage tray and flows into the measuring bucket. The following steps summarize the bucket/stopwatch flow rate measurement process .
1. Ensure that the rubber ball valve in the base of the bucket is open. The valve is operated by rotation of a steel disc at the end of the valve crankshaft.
2. Add appropriate masses to the weigh beam.
3. Using a stop watch, measure the elapsed time between closing the valve and accumulation of a convenient quantity of water in the bucket as indicated by tipping of the weigh beam.
Care should be taken that the bucket does not overflow at high flow rates. Open the drain valve as soon as the stop watch has been stopped. For the most accurate measurements, the timing should be made between two mass values. For example, the stopwatch could be started when the weigh bar, holding a 5 kg mass, first tips. A second weight would then be added to the weigh bar (10 kg, for instance) and the stopwatch stopped when the weigh bar tips a second time. The mass flow rate is then determined by
 (7)
(7)
Alternatively, a rotometer may be installed in series with the Pipe Bends and Fitting Apparatus allowing direct measurement of the flow rate.
Analysis
As shown in equation 6, minor head losses are expressed as functions of the velocity squared. Constants in this expression may be grouped together such that the equation may be written as
![]() (8)
(8)
where k2 = K/2g
Minor loss coefficients can be determined through a curvefit of the experimental data, using a power equation form. The constant resulting from the curvefit procedure would then be used to evaluate the minor loss coefficient. The best value for K is obtained by curvefitting the experimental data with a power equation in which the exponent is set equal to 2.
Friction factor and head loss for the straight section of pipe may be determined directly from equation 1.
Procedure
1. Determine the barometric pressure and the water temperature.
2. Open both the globe valve and the gate valve on the test panel.
4. Open the pump inlet valve to its fully open position. This valve should remain fully open at all times.
5. Open the valve on the instrument panel (main control valve). This valve should be used to control the flow rate during the experiment.
6. Start the pump. Use the speed controller and the main control valve to establish a steady flow. Remove all air bubbles from the system.
7. Select two of the fittings across which pressure drop measurements are to be made. These may already be selected by the instructor. Connect manometer tapping points immediately preceding each fitting under test to the left hand tube of each pair of manometers using the flexible tubing.
8. Connect manometer tapping points immediately after each fitting under test to the right hand tube of each pair of manometers using the flexible tubing. Remove all air from both sections of flexible tubing.
9. Observe the flow rate using either the rotometer (if it is placed in series with the pipe system) or the bucket/stopwatch method. See Flow Rate Measurement section.
10. Open the stop-cocks of the manometer tappings being used.
11. When the level in the manometers are steady, note the difference in water levels between the two tubes of the manometers.
12. Repeat steps 9 to 11 for various values of flow rate. The flow rate may be varied using the speed controller of the pump.
13. Close the stop-cocks on the manometer tappings.
Data Reduction and Questions
1. Determine the loss coefficients for the two fittings at the various flow rates tested. Compare and discuss the experimental loss coefficients with values given in the literature.
2. Determine the loss coefficients for the two fittings by performing a curvefit to power equation form. Compare and discuss the experimental loss coefficients obtained with values in the literature.
3. Are the loss coefficents constant? Discuss how these values might change for different flow rates, Reynolds numbers, and pipe size (diameter).
4. Determine the equivalent length of pipe for each loss coefficient using values of the friction factor obtained for with the expected result from theory and the Haaland eqtn (eqtns 3 & 4).
5. Using your knowledge of manometers, demonstrate whether the difference in elevation of the pressure taps must be considered in reading the difference in manometer height to find the pressure drop caused by the fittings.
References
1. White, F.M., Fluid Mechanics, 2nd Ed., McGraw-Hill Book Co., New York, 1986.
2. Colebrook, C.F., "Turbulent Flow in Pipes, with Particular Reference to the Transition between the Smooth and Rough Pipe Laws," J. Inst. Civ. Eng. Lond., vol.11, pp. 133-156, 1938-39.
3. Haaland, S.E., "Simple and Explicit Formulas for the Friction Factor in Turbulent Pipe Flow," J. Fluids Eng., pp. 89-90, March 1983.
4. Holman, J.P., Experimental Methods for Engineers, 4th Ed., McGraw-Hill Book Co., New York, 1984.
5. G. Cussons Ltd., "Cussons Losses in Pipe Bends and Fittings - Apparatus Type P6125," Technical Manual 2/80/6125, Manchester, England, 1980.