** STILL UNDER CONSTRUCTION, THE CONTENT WILL BE UPDATED AND EXTENDED **

Computer resources used in this group include resources obtained through NSF/IMR-0414903 and from the Louisiana Optical Network Initiative (LONI)
RESEARCH PROJECTS
Nanoparticle delivery to tumor tissue
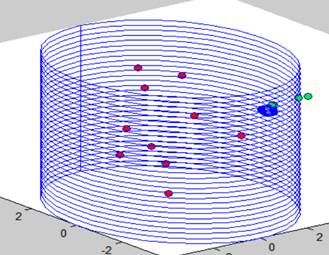
A blood vessel section is represented as a cylinder and a single pore is added to it. Nanoparticles are assumed to move dragged by the plasma but is also animated with Brownian motion due to collisions with other particles. Thus, a monte carlo approach is implemented where the particles moves a distance consistent with the velocity profile of the fluid, plus a random displacement due to Brownian motion. Near the pore, a drift current push particles into the pore. This model can predict the delivery efficiency as a function of blood pressure, pressure gradient across the pore, nanoparticle concentration in blood, speed profile, nanopore size, blood vessel radius, and nanoparticle radius. Some of the main results indicate that the delivery of nanoparticle increases with blood pressure and particle concentration but it is more sensitive to the later, however, the percentage of nanoparticles delivered, decreases with increasing concentration, this is an interesting results that need to be experimentally verified. This work is supported by the Louisiana Alliance for Simulated Guided Materials Applications LASiGMA
		Conductive Polymers
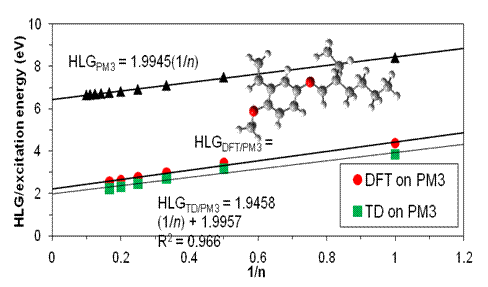
	We use a quantum chemistry techniques to calculate a number of electronic and geometrical properties of oligomers and polymers. The main approach consists on calculating these properties as a function of the number of units in the oligomer and use extrapolation techniques to infer the corresponding property of the polymers. One of the main findings is that the extrapolation criteria depends on the method used to optimize the oligomer’s geometry. Particularly, we found that if semiempirical geometries are used, the HLG converges to within experimentally measured band gap when a HLG vs. the inverse of number of monomers, is extrapolated using a linear function. Instead, when DFT geometries (using the hybrid B3PW91 functional) are used, the HLG extrapolates o the band gap when an exponential function of the number of units is used instead. This work was partially supported by the Louisiana Board of Regents and NSF through grants NSF(2008)-PFund-106 and LEQSF(2009-12)-RD-A-27