<< Back to BIEN 435 Course Rules
Analysis of Thermal
Dilution Method for Cardiac Output Measurement
Last Updated December 6, 2004
One method
for measurement of cardiac output is to inject cold saline into the right
atrium of the heart and determine how long it takes for the dye to wash
out. A thermistor is placed in the
aorta, and temperature is measured as a function of time. The method can be analyzed through a
There are
two questions to be answered: 1) How
does the temperature change with time? and 2) How is flow rate related to the
temperature measurement?
 The following analysis will use
concentration instead of temperature because the nomenclature is simpler. However, the equations are otherwise the
same.
The following analysis will use
concentration instead of temperature because the nomenclature is simpler. However, the equations are otherwise the
same.
1) Temperature as a function of time:
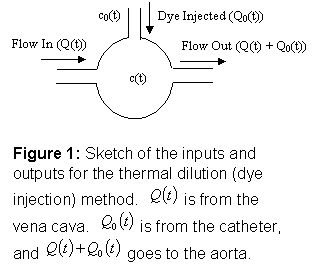
The
experiment is sketched in Figure 1.
"Flow
In" is the blood recirculated through the vena cava. "Flow Out" is the blood into the
aorta. "Dye Injected" is the
dye injected through a catheter into the right atrium. The entire four chambers of the heart are
modeled as a single mixing chamber. It
is assumed that the injected dye mixes completely and immediately with the
blood from the vena cava. The
conservation of mass states that the difference between mass in and mass out
results in a change of mass within the chamber.

(i.e. if 1
mg/s of dye flows in and only 0.7 mg/s flows out, then the dye in the chamber
increases at a rate of 0.3 mg/s). Define the following variables:
c(t) concentration of the dye in the chamber
V volume of the chamber
c0 concentration of the dye injected
Q0(t) flow rate of the injected dye into the
chamber
Q(t) flow rate out of the chamber
The rate of
mass in is c0Q0
(g/ml x ml/s => g/s).
The rate of
mass out is c(Q(t) + Q0(t))
Since the
mass in the chamber is cV and V is constant, the rate of change of mass in the
chamber is V dc/dt.
Therefore,
the equation governing the concentration is:
![]()
Which can
be rearranged to a more familiar form:
![]()
![]() is the cardiac output we are trying to measure. It is thus an input to the equation. It is, of course, a function of time, but we
can approximate it as a constant if we decide to look at time scales larger
than one cardiac cycle.
is the cardiac output we are trying to measure. It is thus an input to the equation. It is, of course, a function of time, but we
can approximate it as a constant if we decide to look at time scales larger
than one cardiac cycle. ![]() is the flow rate of injection, and is also an input. In general,
is the flow rate of injection, and is also an input. In general, ![]() , so it can be ignored on the left hand side (but not on the
right hand side). The equation then
reduces to.
, so it can be ignored on the left hand side (but not on the
right hand side). The equation then
reduces to.
![]()
![]()
The form of
this equation is identical to that of a charging RC circuit. Compare it to:
![]()
 Thus,
we already know how this equation is going to behave. The solution has the same form as the RC
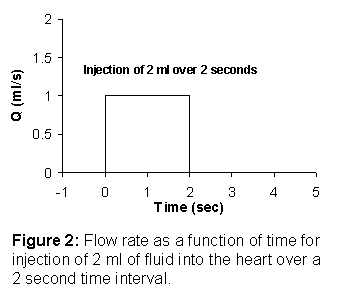
circuit, with the RC time constant replaced by V/Q. Assume that the fluid is injected from the
catheter as a pulse, as shown in Figure 2.
Mathematically this can be expressed as
Thus,
we already know how this equation is going to behave. The solution has the same form as the RC
circuit, with the RC time constant replaced by V/Q. Assume that the fluid is injected from the
catheter as a pulse, as shown in Figure 2.
Mathematically this can be expressed as ![]() , where
, where ![]() is the unit step
function,
is the unit step
function, ![]() is a constant
numerically equal to 1 for the example in Figure 2 and
is a constant
numerically equal to 1 for the example in Figure 2 and ![]() is the total time of
injection, equal to 2 for the example in Figure 2. To find concentration in the aorta as a
function of time, one must solve Equation 1 with the expression for
is the total time of
injection, equal to 2 for the example in Figure 2. To find concentration in the aorta as a
function of time, one must solve Equation 1 with the expression for ![]() substituted on the
right hand side, which is:
substituted on the
right hand side, which is:
![]()
The
equation can be transformed to the
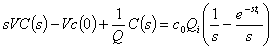
where the
second term on the left hand side is zero because the initial concentration in
the aorta is zero, and the second term on the right hand side comes from the
shifting theorem. The algebraic
manipulation yields:
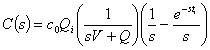
The inverse
transform is more obvious if this equation is rewritten as:
 .
.
The ![]() factor is a time delay. The inverse transform of
factor is a time delay. The inverse transform of ![]() can be found in the
tables of
can be found in the
tables of
![]()
Thus,
![]()
So with ![]() it follows that the
inverse transform of
it follows that the
inverse transform of ![]() is:
is:
![]() .
.
The term
modified by ![]() looks like the
charging of a capacitor in an RC circuit.
The term modified by
looks like the
charging of a capacitor in an RC circuit.
The term modified by ![]() looks like the
discharging of an RC circuit. Therefore,
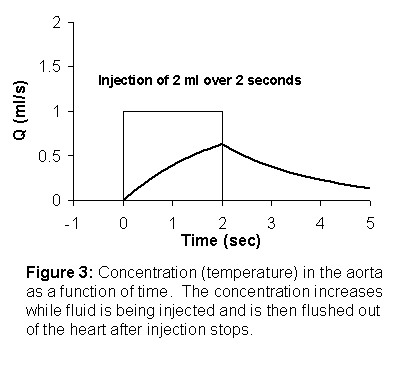
the response to the dye sensor in the aorta (or thermistor in the case of
thermal dilution is as shown in Figure 3.
During injection, the concentration in the aorta increases. Once injection stops, the dye is flushed out
of the heart in a manner similar to the discharging of a capacitor. It is instructive to rewrite the equation for
looks like the
discharging of an RC circuit. Therefore,
the response to the dye sensor in the aorta (or thermistor in the case of
thermal dilution is as shown in Figure 3.
During injection, the concentration in the aorta increases. Once injection stops, the dye is flushed out
of the heart in a manner similar to the discharging of a capacitor. It is instructive to rewrite the equation for
![]() for times greater than
or equal to
for times greater than
or equal to ![]() , when both of the step functions are active and then reshift
the time base back so that it starts at
, when both of the step functions are active and then reshift
the time base back so that it starts at ![]() . In this case, the
equation becomes:
. In this case, the
equation becomes:
![]()
 This form shows that after
This form shows that after ![]() the system is simply
“discharging” all of the dye that was injected up to that time. That is, there is an
the system is simply
“discharging” all of the dye that was injected up to that time. That is, there is an ![]() decaying exponential
with an amplitude factor of
decaying exponential
with an amplitude factor of ![]() (which is a constant,
independent of time).
(which is a constant,
independent of time).
BIEN 435
Last Updated December 6, 2004
Steven A. Jones