Vector Concepts for Fluid Mechanics
1.
A vector has
magnitude and direction and can be described as an arrow pointing in the
assigned direction with a length equal to its magnitude (Figure 1).
2.
Vectors can be
described in Cartesian coordinates as:
3.
The coefficients 
, 
, and 
are the 
, 
, and 
components of the
vector.
4.
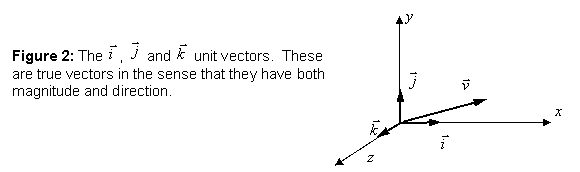
are
themselves vectors. 
is
a vector pointing in the direction, 
is a vector pointing
in the 
direction, and 
is a vectory pointing in the direction. See Figure 2.
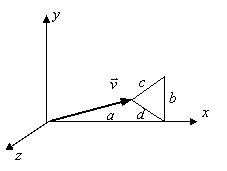
5.
The magnitude of
a vector is its length, which is given by:
,
which is
simply a statement of the Pythagorean theorem.
Problem 1:
Given that the vector can be represented as 
, show that the magnitude of is 1.
Problem 2:
Show that the equation for the magnitude of a vector is simply a statement of
the Pythagorean theorem as follows. First note that and are perpendicular to
one another because is parallel to the axis and is parallel to the axis. Use the Pythagorean theorem to obtain 
in terms of and . Now, since and are both perpendicular
to the axis, is also perpendicular
to the axis (i.e., it lies in
a plane that is perpendicular to the axis. Use this information to write the length of
the vector 
in terms of and . Then back substitute
for to obtain the length
of in terms of , and .
6.
The dot product
between two vectors, 
and 
is
7.
The dot product
is a scalar value.
8.
The value of the dot
product is 
, where 
is the angle between
the two vectors.
9.
The dot product
of one vector with another is physically the projection of that vector on the
other vector, multiplied by the length of the other vector.
10. A unit vector is a vector with magnitude of one.
11. Any vector can be normalized to become a unit vector
by simply dividing by its own magnitude.
.
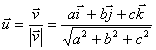12. Recalling 9 above, the dot product of any vector with
a unit vector is the projection of that vector in the direction of the unit
vector. (e.g., the shadow cast by the
vector by a light source that is in the plane of the two vectors and that is
perpendicular to the unit vector).
13. The cross product of two vectors is a vector
and can be written as:
14. 
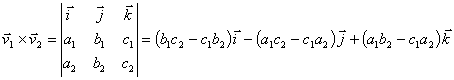
15. The magnitude of the cross-product has the
value of 
, where is the angle between
the two vectors.
16. The direction of the cross-product is
perpendicular to both of the two original vectors, or, equivalently,
perpendicular to the plane in which the two original vectors lie.
17. The above concepts are ones that students should know
from their statics course. The students will need this much review, and
they will need to be reminded that they already know these concepts from statics. Next come
some concepts that will be new in the sense of understanding vector
applications. In other words, while
students may have seen the gradient operator in their math class, they may not
yet understand what it means physically.
18. The gradient of a function 
is defined as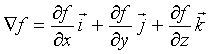 
.
19. The gradient is a vector.
20. However, the function itself is not a vector in
this case.
21. The gradient is a function of the spatial coordinates.
22. Each term of the gradient is the rate of change of the
function as one moves in the given coordinate
direction, assuming that there is no change in position with respect to the
other two coordinate directions. To
illustrate the gradient, consider the situation shown in Figure 4. A paper mill produces a sulfurous odor that
diminishes in pungency with distance from the mill. A person at point A experiences a relatively
large rate of reduction of the odor as he moves in the direction. The same person experiences a relatively
small rate of reduction of odor as he moves in the direction. Thus, the component of the
gradient is large and the y component of the
gradient is small.
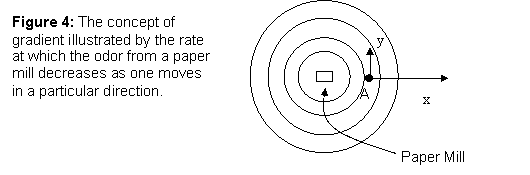
Problem 3: Assume in the
paper mill example that the odor drops off with distance from the mill
according to the equation 
. Give the equation
for the gradient at any location 
from the mill,
assuming that the origin of the and axes is at the center
of the mill. Hint: You should write 
and then take the
derivatives with respect to and . Answer: 
.
Problem 4: For the same paper
mill, what are the and components of the
gradient found in Problem 3 at a point 
? How do they agree
with the above statement that the odor should drop off more quickly along the direction than along
the direction?
23. Velocity is a vector quantity. It’s magnitude is
the speed of an object. It’s direction is the direction in which the object is
moving.
24. The gradient operator can be described as a
vector, 
. Thus, the gradient
of a function is the gradient operator applied to the function.
25. The divergence of a vector (such as velocity) is
the dot product of the gradient operator with the vector.
26. The divergence is a scalar quantity because it is a
dot product.
27. One may take the divergence of the gradient of a
function. This scalar quantity is
known as the Laplacian operator.
28. One may also consider the divergence to be an operator
defined as:
29. Thus,
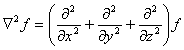
30. The curl of a vector is the cross-product of the
gradient operator with the vector.
31. The curl of a vector is another vector.
32. The curl of a vector can be written as:
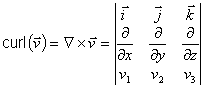
and this form provides one with an easy way to remember
where the “–“ signs must go.
Problem 5: Which of these are
not legitimate vector operations. Why?
Assume 
is a scalar
function.
