Statistical Testing

Introduction

Statistical testing is performed to determine how confident one can be in reaching conclusions from a data set. It is highly important in biological experiments because these often lead to data sets with wide variability.

A population is a group under study. For example if you are interested in comparing men to women, men would be one population and women would be another.

There are several types of statistical testing. The test chosen depends on the hypothesis you are testing. For example, the student’s T test is used to determine whether, on average, the mean value of some variable of interest (e.g. height, age, temperature) in one population is different from the mean value of the same variable in another. For example, examine the question “On average, are men taller than women?” Here the variable of interest is height, the populations are men and women, and the statistic of interest is the average height.

Each statistical test yields a p value (short for probability value) that represents the probability that the null hypothesis is correct. The null hypothesis is generally the opposite of what you are trying to prove. For example, you could formulate the hypothesis that Biomedical Engineers perform better on the FE exam than Industrial Engineers. The null hypothesis is:

Biomedical Engineers do not perform better on the FE exam than Industrial Engineers.

Exercise 1: Identify the population, the variable of interest and the statistic of interest implied by the above null hypothesis.

If you do a T-test and obtain a p value of 0.05, it means that:

“Given the standard deviation of these data and the number of data points, there is a 5% probability that we would obtain a difference in the means this large or larger if the performance of Biomedical and Industrial Engineers were exactly the same.”

In other words, given this data set, we have only a 1 in 20 chance of being wrong if we claim that Biomedical Engineers perform better on the FE exam than Industrial Engineers.

Be careful in interpreting statistical tests. The natural thing to think is that if your p-value is less than the designated value (in biological applications this is usually taken as 0.05) then your hypothesis is true. Some dangers are:

1. If you do enough statistical tests on something, the odds are that the t-test will show significance on something even though significance is not there. For example, if p=0.05 is taken as the cutoff point, then 1 time out of 20 you will get significance when the underlying distributions are the same. Thus, if you perform 20 t-tests, odds are that one of them will show significance even though no significance exists.

2. If the p value exceeds 0.05, it does not prove the null hypothesis. Indeed you can never prove the null hypothesis. If your hypothesis is that Burmese cats weigh more than Siamese cats and you find no significance (p > 0.05), it does not prove that Burmese cats and Siamese cats weigh the same. It only means that there is not enough evidence in your data set to state with confidence that they have different weights.

Some Often-Used Statistical Tests

Chi-Squared Test

This is used to test the hypothesis that the data you are working with fits a given distribution. For example, if you want to determine whether the times of occurrence of meteorites during the Leonid meteor shower are inconsistent with a Poisson distribution, you could formulate the null hypothesis that the arrival times follow such distribution and test whether the data contradict this null hypothesis.

A Chi-Squared test is typically the first test you would like to perform on your data because the underlying probability distribution determines how you will perform the statistical tests. Note, however, that you cannot prove that the data follow a given distribution. You can only show that there is a strong probability that the data do not follow the distribution.

F-test

You choose two cases of something and formulate the hypothesis that the variances of the variable of interest for populations are different. For example, assume that you have two tools to measure height and you want to know if one leads to more consistent results than the other. You could collect repeated measurements of some item from both of these tools and then apply an F-test. (The two populations in this case are 1. measurements taken with the first tool and 2. measurements taken with the second tool). Note that in the T-test it matters whether the variances of your two data sets are different. Therefore, it is a good idea to perform an F-test on your data before you perform a T-test.

T-test

This test is probably the most widely known of all the statistical tests. You choose two populations and formulate the hypothesis that they are different. For example, if you would like to know if Altase (a blood pressure medicine) reduces blood pressure, you could form the hypothesis that “People who are given Altase (population 1) will have lower blood pressure than people who are given a placebo (population 2).

Linear Regression and Pearson’s Correlation Coefficient

Another hypothesis might be that one variable is correlated with another. For example, “Blood pressure is correlated with the number of cigarettes smoked per day.” In this case you would do a linear regression of the blood pressure vs number of cigarettes smoked and examine the p-value for this regression. This test is different from the T-test in that you are looking at a functional relationship between two quantitative values rather than a difference in means between two cases. The p value depends on the r value (which is Pearson’s Correlation Coefficient) for goodness of fit of the regression and the number of data points used in the regression. When you perform a least squares fit in Excel, one of the parameters that the software provides in the output is the p value.

Anova

The Anova examines the variance within each population and compares this to the variance between populations. The simplest case is where there are three populations, and you wish to determine whether some statistic varies from population to population. If you were interested in determining whether FE exam scores differed for Biomedical Engineering, Industrial Engineering and Mechanical Engineering students, this would be the test to use. It can also be used for cases where you do not expect a linear correlation but do expect some effect of a given variable. Weight, for example generally increases as one ages, but then typically diminishes in old age. The trend is not linear, but it certainly exists. For example, look at the variability of blood pressure as a function of age. The categories are obtained by dividing the subjects into specific age groups, such as 20-30, 30-40, 40-50, 50-60, 60-70, and 70-80 years old.

More details of each statistical test are provided later in this document.

Probability Distributions

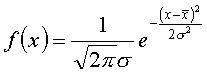
We denote the probability distribution of a random number by f(x). F-Tests and T-Tests assume that the probability distribution of the noise in the data follows a Gaussian (or normal) distribution, 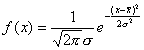. The rand() function in Excel generates a uniformly distributed random variable between 0 and 1. This means that the number is just as likely to fall between 0.2 and 0.3 as it is to fall between 0.3 and 0.4, or between 0.9 and 1. The Gaussian distribution and uniform distribution are shown in Figure 1. The area under both curves must equal 1, which means that it is assured that the value of a given experiment will be somewhere in the possible range. For example, if the experiment is the roll of a die, the result must be one of 1, 2, 3, 4, 5, or 6. Hence, the probability of the result being 1, 2, 3, 4, 5, or 6 is 1.

The Gaussian distribution is important because many distributions are (at least approximately) Gaussian. The “central limit theorem” states if one takes the average of n samples from a population, regardless of the underlying distribution of the population, and if n is sufficiently large, the distribution of this mean will be approximately Gaussian with a mean equal to the mean of the original distribution, and a standard deviation of approximately: .

Example 1: Show that when a new random variable is defined as “the sum of the values when a die is thrown three times,” the probability distribution begins to take on the shape of a Gaussian distribution.

Solution: First look at the probabilities for the sum of two dice. Anyone who has played Monopoly is aware that 2 or 12 occur with low probability, whereas a 7 is the most likely number to be thrown. Table 1 demonstrates all possible combinations of Throw 1 and Throw 2. Note that there is one way to obtain a “2,” 2 ways to obtain a “3,” 3 ways to obtain a “4,” 4 ways to obtain a “5,” 5 ways to obtain a “6,” 6 ways to obtain a “7,” 5 ways to obtain an “8,” 4 ways to obtain a “9,” 3 ways to obtain a “10,” 2 ways to obtain an “11,” and 1 way to obtain a “12.”

Put Table 1 here

It follows that the distribution for 2 rolls of a die is trianglular in shape. Table 2 builds on this result. On the left of the table are the possible outcomes for Throw 3, and at the top of the table are the possible outcomes for the combination of throws 1 and 2. At the bottom of the table, the row marked “Frequencies” shows the frequency for each outcome. For example, the 6 at the bottom indicates that there are 6 different ways to obtain 7 from the roll of 2 dice.

Put Table 2 here

To obtain the number of combinations for each possible result, it is necessary to multiply the number of times a given number occurs in each column by the frequency for that column and then sum over all columns. For example, the number of possible 8’s 1+2+3+4+5+6 = 21. The total number of possible combinations is 63 = 216, so the odds of obtaining an 8 are 21/216. Table 3 shows all combinations that can occur for 3 throws of a die and the number of times they can occur.

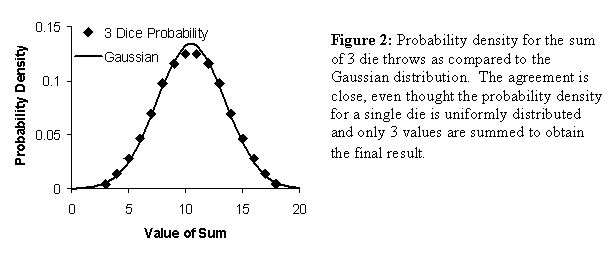
The probability density for the 3 rolls of a die are obtained by taking the frequency values in Table 3 and dividing by the total possible number of combinations (256). These values are plotted in Figure 2 along with the probability density for the Gaussian. Even when the number of values in the sum is as small as 3, close agreement is found with a Gaussian distribution.

Exercise 2: Define a random number as the number of times a coin comes up heads when tossed 20 times. For example, if the outcome is T, T, T, H, T, H, H, H, T, H, T, H, T, H, H, H, T, T, T, T, there are 9 heads and 11 tails, so the random number’s value is 9. This is the same as defining H as 1 and T as zero and defining a new random variable as the sum results from all 20 tosses. Find the probability density function for this new random variable and compare it directly to a Gaussian distribution. (Hint: for 1 toss the probability density is 0.5 at 0 and 0.5 at 1. For 2 tosses, there is one way to obtain a value of 0 (two tails), two ways to obtain a value of 1 (H, T and T, H) and 1 way to obtain a value of 2 (two heads). The density is 0.25 at 0 and 2 and 0.5 at 1. For 3 tosses, there is a 50% chance of all values remaining the same (the 3rd toss is tails) and a 50% chance of them increasing by 1. Thus, the possibilities are given by Table 4:

Page 11:

Example 4: John Q. Researcher proposes that a person’s blood pressure is linearly proportional to the person’s car’s gas mileage. He surveys 10 people and collects the data to the right. Is this survey consistent with the hypothesis within the p < 0.01 range?

Solution: The easy way to do this is to input the data values into Excel and perform a linear regression. Select “Tools | Data Analysis” and then click on “linear regression.” (If the Data Analysis menu does not appear see the Help menu under “regression” for instructions on how to get it to appear). Fill in the requested data (cells for y-range, cells, for x-range, and cells for output) and hit “OK.” The output should look like the data in the tables below (although not quite as pretty):