Duality
The term
“duality” refers to the ability to treat two different types of problems
identically as a result of their differential equations being identical. Consider, for example, the equation for the
simple LRC circuit:
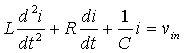
Now
consider the equation for velocity of a mass on a spring, with damping:

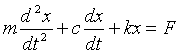
![]()
Mathematically,
the two equations are the same. The only
difference is in the names of the parameters.
Damping
corresponds to resistance. V=iR
corresponds to F=cv.
The spring
corresponds to a capacitor. q=CV
corresponds to x=F/k.
The mass
behaves like an inductor. V=Ldi/dt
corresponds to F=m dv/dt.
It is not
surprising, then, that inductance is sometimes called “inertance,” in analogy
to the inertia of a mass. Some other
things to consider are:
1. Regardless of the force at time t=0,
a mass initially at rest will have a velocity of zero at t=0. Similarly, the current in an inductor cannot
change instantaneously. This is what
inertia really means; an object will keep moving unless it is operated on by a
force over some time period.
2. In contrast, the charge on a
capacitor or the displacement of a spring can, in theory, change
instantaneously if the force changes instantaneously.
3. For a damper, velocity can change
instantaneously, but displacement cannot.
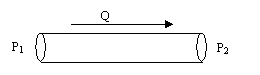
A third
example of duality is in Fluid Flow.
Consider a tube, as shown to the right, and the relationship between
pressure and flow rate.
![]()
There are
three phenomena that affect the relationship between flow and pressure. The first is a resistance caused by
viscosity. You will learn about this in
fluid mechanics. For this phenomenon,
pressure is directly proportional to flow rate.
The second
phenomenon is the expanding of the tube as a result of the pressure. This actually obeys a non-linear
relationship, but if the tube doesn’t expand too much, it can be approximated
linearly:
![]()
 This simply says that an increase in
pressure will cause the walls to stretch and thus make the volume inside the
tube larger. This is just like a
capacitor, with volume being charge and pressure being voltage, that is
This simply says that an increase in
pressure will cause the walls to stretch and thus make the volume inside the
tube larger. This is just like a
capacitor, with volume being charge and pressure being voltage, that is ![]() . Note that for the
capacitance, the
. Note that for the
capacitance, the ![]() is across the tube wall, not from one end of the tube to the
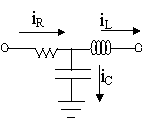
other. Thus, this is analogous to having
a capacitor shunted to ground, like the figure to the right.
is across the tube wall, not from one end of the tube to the
other. Thus, this is analogous to having
a capacitor shunted to ground, like the figure to the right.
If this is
an aorta, then ![]() implies that
implies that ![]() . In other words, the
“current” in the capacitor is the rate at which blood is being stored in the
aorta as a result of the increased vessel diameter.
. In other words, the
“current” in the capacitor is the rate at which blood is being stored in the
aorta as a result of the increased vessel diameter.
The value
of the capacitance can be deduced from the definition ![]() , analogous to
, analogous to ![]() . Lets assume that a
pressure change from systole to diastole changes the radius of the aorta by
10%. Then
. Lets assume that a
pressure change from systole to diastole changes the radius of the aorta by
10%. Then ![]() (i.e. the volume at
higher pressure minus the volume at lower pressure). The change in pressure is just
(i.e. the volume at
higher pressure minus the volume at lower pressure). The change in pressure is just ![]() , which might be 120 mmHg – 80 mmHg = 40 mmHg for a normal
human. (Note that 1 mmHg is equal to
1330 dynes/cm2). It is thus
an easy matter to solve for C with:
, which might be 120 mmHg – 80 mmHg = 40 mmHg for a normal
human. (Note that 1 mmHg is equal to
1330 dynes/cm2). It is thus
an easy matter to solve for C with:
![]()
The third
phenomenon is the inertia of the fluid.
Balancing forces we get that:
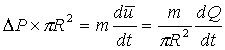
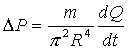
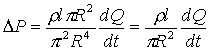
But since ![]() ,
,
So the
inductance in this case is ![]() .
.
It is
legitimate to ask where the capacitor and inductor really belong in the
circuit. The tube does not consist of a
resistor followed by a capacitor to ground followed by an inductor. The resistance, capacitance, and inductance
are all distributed throughout the tube.
In circuit theory, this can be modeled as a transmission line, which
ends up providing wave solutions. In
vascular fluid mechanics, wave phenomena occur as well, and these have been
heavily studied. However, if the overall
interest is to understand what the general flow rates are in the arterial
system, one can use the model pictured above for each segment of the artery
tree, combine these elements as appropriate, and solve the simple circuit
equations.
You may
also hear about “acoustic” impedance.
There is an analogy between acoustics, which deals with pressure and
velocity within a medium, and the RLC circuit.
However, the analogy is not as strong as that with mechanical
impedance. For a plane wave, it can be
shown that the pressure is directly proportional to rc u,
where r is the density of the medium, c is the speed of sound in
the medium (assumed constant), and u is the velocity of the air
disturbance. One can, of course, talk
about the mass of the medium (inertia) and about the compressibility of the
medium (capacitance). However, the
acoustic impedance does not relate to a pressure drop across some element. In fact, classical acoustics leaves out
damping, which would correspond to resistance.
Acoustic impedance relates more to the reflection of acoustic waves from
surfaces. This is exactly the phenomenon
exploited in ultrasound. Any time a
sound wave hits an interface within the body where the sound speed changes, a
wave is reflected back. The time
required for the wave to reach the receiver indicates the depth of the
interface. The larger the impedance
mismatch, the stronger the reflected signal.
The interface between tissue and blood, for example, generally provides
a strong ultrasonic signal.
Exercises
Exercise 1:
Poiseuille’s
equation describes the pressure drop in a long pipe as follows:
![]()
Where ![]() is the cross-sectional averaged velocity equal to
is the cross-sectional averaged velocity equal to ![]() , r0 is
the radius of the pipe, m is the dynamic viscosity, and L is
the length of the pipe. Use this
relationship to derive a formula for flow resistance, R, as defined by the
equation
, r0 is
the radius of the pipe, m is the dynamic viscosity, and L is
the length of the pipe. Use this
relationship to derive a formula for flow resistance, R, as defined by the
equation ![]() . Based on this
approach, what is the resistance of a) two pipes of lengths L1 and L2 and radii r01
and r02 in series, and b)
two pipes of lengths L1
and L2 and radii r01 and r02 in parallel.
. Based on this
approach, what is the resistance of a) two pipes of lengths L1 and L2 and radii r01
and r02 in series, and b)
two pipes of lengths L1
and L2 and radii r01 and r02 in parallel.
Exercise 2:
Sometimes
it is not possible to make a direct comparison between fluid mechanical and
electrical elements. Consider the case
of flow in a venturi (a narrowing in a tube—medically this is called a stenosis
if it is in the artery). The equation
looks like ![]() , where
, where ![]() is the blood density
and CL depends on the
geometry of the stenosis. The ratio
is the blood density
and CL depends on the
geometry of the stenosis. The ratio ![]() now depends on the
value of Q. The best approach in this case is to pick a
point around which you expect Q to
vary and define the resistance as the rate of change of P with respect to Q
(i.e.
now depends on the
value of Q. The best approach in this case is to pick a
point around which you expect Q to
vary and define the resistance as the rate of change of P with respect to Q
(i.e. ![]() ).
).
A. Take the derivative of the
expression for ![]() above to obtain a
relationship for this definition of R.
above to obtain a
relationship for this definition of R.
B. How does it compare with what you
would get if you simply divided the equation by Q?
C. Which method is “correct” and why?
D. Draw a plot of the relationship
between pressure and flow, and draw two straight lines that indicate the two
possible definitions of R. You may pick whatever values you wish for ![]() , CL,
and Q.
, CL,
and Q.
Steven A. Jones
BIEN 402, Biomedical
Senior Design