Dimensional Analysis
Reynolds Number
The Reynolds Number 
is regularly cited as
the most important parameter in fluid mechanics. You have seen that this number can be used to
predict whether flows will be laminar or turbulent, but the full significance
of this and other non-dimensional combinations of parameters may not yet be
completely understood. It is the purpose
of this document to discuss the following aspects of these parameters:
1.
Why is it useful
to describe problems in terms of non-dimensional parameters?
2.
How does one
determine which non-dimensional parameters to use?
3.
What is the
relationship between such non-dimensional parameters and the governing
differential equations?
4.
How can one apply
these parameters to solutions of differential equations?
1.
Why is it useful
to describe problems in terms of non-dimensional parameters?
Consider first the case of
the simple RC electrical circuit. The
ratio of output voltate (
) to input voltage (
) is given by the following relationship:
.
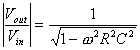Assume that you did not know
this relationship and that you needed to measure the response of all possible
RC circuits. One way to do this would be
to measure the output while varying each of , 
, 
, and 
. Assume that you can
get away with looking at 10 values of each parameter. Since you need to vary 4 different
parameters, you must make 10,000 measurements, which means that you will be in
the instrumentation laboratory for a long time, and you will probably miss the
homecoming game. However, a dimensional
analysis of the system will indicate that there are only two parameters that
are independent of one another. One of
these is the voltage ratio, 
, and the other is the non-dimensional parameter 
. Recall that 
has the dimensions of
time and that has the dimensions of
1/time, indicating that the product is non-dimensional. Thus, it is necessary to vary only one
parameter and measure the other (). You could take 3
times as many meaningful measurements and still be out of the lab in a time
that is orders of magnitude shorter. Not
only will you be able to make it to the homecoming game, but you will also have
time to stop by the Huddle House and have a cup of coffee beforehand. The analysis tells you that it is not even
necessary to change the resistance and capacitance values of the circuit. You can change simply by changine .
2.
How does one
determine which non-dimensional parameters to use?
The student should refer to
section 7.7.1 in Middendorf and Engelmann for a
discussion of the Buckingham p
theorem. The theorem describes a method
to determine how many dimensionless parameters will be important in a problem
given the dimensional parameters.
Because this type of analysis can be applied to any physical problem
without the need to understand the governing differential equations, the
student must be capable of performing it.
Exercise 1:
Use the Buckingham Pi theorem to show that the two non-dimensional parameters
of importance to the RC circuit described above are and . You will need to
express ohms as volts/amp and capacitance as amp-s/volt.
Exercise 2:
Use the Buckingham Pi theorem to determine the important non-dimensional
parameters for an LRC circuit.
Exercise 3:
Assume that you are given an RC circuit, but that the resistance is a function
of current, i.e. 
. Determine the
important non-dimensional parameters governing the circuit.
3.
What is the
relationship between such non-dimensional parameters and the governing
differential equations?
Non-dimensionalization
of the Navier Stokes equations
4.
How can one apply
these parameters to solutions of differential equations?
Derivation
of Poiseuille flow.