LAB 5 - One-Dimensional Fin Heat Transfer
Introduction
A fin is an extended surface that is used specifically to enhance the heat
transfer rate between a solid and an adjoining fluid. There are several different
general fin configurations, including straight fins, which are extended surfaces
attached to plane walls and annular fins that are circumferentially attached
to a cylinder. These fin types may have rectangular cross sections, whose
area may be expressed as a product of the fin thickness t and the width w
for straight fins or the circumference for annular fins.
As previously indicated, the primary interest when analyzing fin performance
is a determination of the enhancement of heat dissipation from a surface
to the surrounding fluid. In order to determine the heat transfer rate from
a fin, the temperature distribution along the fin must first be determined.
The temperature distribution may be determined analytically if several
simplifying assumptions are made. One-dimensional heat transfer in the
longitudinal (x) direction is typically assumed, even though heat conduction
within the fin is two-dimensional. The rate at which energy is convected
to the surroundings from any point on the fin must be equivalent to the heat
conducted to that point in the transverse (y, z) direction. However, since
most fins are thin, the temperature changes in the x-direction are much greater
than those in the transverse directions. Therefore, the temperature gradients
in the y and z directions may be assumed to be negligible, and the analysis
becomes one-dimensional. Additional assumptions include: steady state conditions,
constant thermal conductivity, negligible radiation from the surface, no
heat generation within the fin, and that the convection heat transfer coefficient
h is uniform over the entire surface. With these assumptions, an application
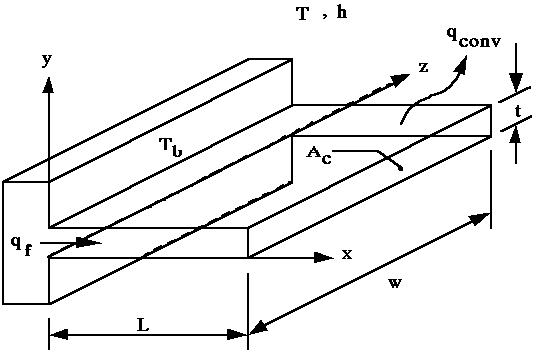
of the conservation of energy principle to the straight fin of uniform cross
section, shown in Figure 1, will result in an ordinary differential equation
that can be solved for the temperature in the fin.

The fin temperature at the base is T(0) =
Tb while the surrounding fluid is at
T![]() . The rectangular
fin has a uniform cross sectional area Ac
= wt. With these physical characteristics specified, the governing differential
equation is
. The rectangular
fin has a uniform cross sectional area Ac
= wt. With these physical characteristics specified, the governing differential
equation is
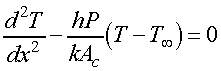
In order to simplify this equation, the dependent variable T may be transformed
by defining an excess
temperature ![]() as
as
(2)
Since T![]() is a constant,
d
is a constant,
d![]() /dx = dT/dx, and equation
1 can now be written as
/dx = dT/dx, and equation
1 can now be written as
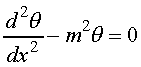
where
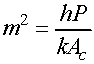
Equation 3 is a linear, homogeneous, second-order differential equation with
constant coefficients. The general solution has the form
(5)
Boundary conditions must be utilized in order to determine the constants
C1 and C2
in equation 5. One of the boundary conditions is a specified temperature
at the base of the fin (x = 0).
(6)
A second boundary condition results from the convection heat transfer from
the fin tip. An energy balance applied to a control surface about the tip
indicates that the conduction to the tip must equal the heat transferred
by convection from the tip to the surroundings.
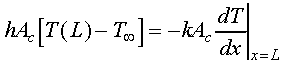
Equation 7 may be restated in terms of the excess temperature,
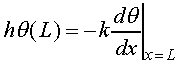
Substituting the general solution, equation 5, into the boundary conditions,
equations 6 and 8, gives the following
(9)
(10)
Equations 9 and 10 may be solved for C1 and
C2. With the constants known, they may be
substituted into the general solution, which, after some tedious algebra,
results in
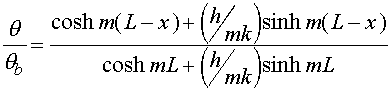
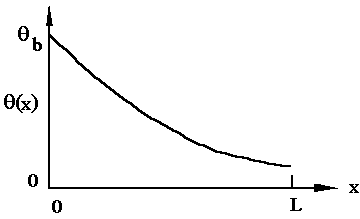
This equation expresses the temperature of the fin as a function of the
longitudinal location. A typical temperature profile is shown schematically
in Figure 2. With the temperature in the fin determined, it is now possible
to calculate the total heat loss from the fin. Note that the heat transferred
into the fin at the base equals the heat loss from the fin. Fourier's law
applied at the base gives
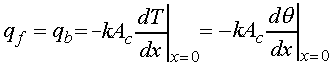
With the temperature distribution known,
qf can then be evaluated, giving
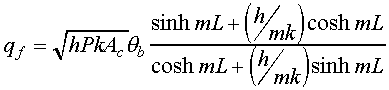
Determination of the Heat Transfer Coefficient
The heat transfer from a rectangular fin can be determine by several means.
An experimental measurement of the heat entering the fin through the base
could be used to determine the fin heat transfer. Alternately, equation 13
could be used, assuming the heat transfer coefficient is a known quantity.
Unfortunately, h is the most difficult of the parameters in the equation
to determine and is usually an unknown. Fortunately, a statistical method
is available that utilizes experimental data representing the temperature
profile in the fin to determine the value of the heat transfer
coefficient.
The method of least squares is a statistical method that can be used in this
case to curvefit the experimental data. The data represents the longitudinal
position (x) and the corresponding temperature (T
or ![]() ) at
that position. Based upon the assumption that the errors in the experimental
measurements follow a Gaussian distribution, the method of least squares
produces a unique value for the constants to be determined. In other words,
the value of the constants determine the best fit of the data, given the
most probable form of the governing equation (the form of the curvefit
equation).
) at
that position. Based upon the assumption that the errors in the experimental
measurements follow a Gaussian distribution, the method of least squares
produces a unique value for the constants to be determined. In other words,
the value of the constants determine the best fit of the data, given the
most probable form of the governing equation (the form of the curvefit
equation).
The form of the curvefit equation
for ![]() (x)
can be extracted from the analytical solution (equation 11). The proposed
curvefit equation is
(x)
can be extracted from the analytical solution (equation 11). The proposed
curvefit equation is
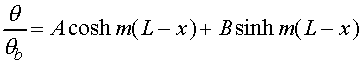
where the values of the constants A and B could be determined from equation
11 as
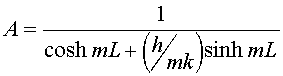
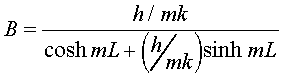
However, the values of A and B may also be found using the method of least
squares. The strategy for fitting the "best" line through the data would
be to minimize the sum of the squares of the residual errors
Sr for all of the available data. The residual,
or error, is the discrepancy between the measured data and the approximate
value predicted by the curvefit equation. The residual for each set of data
(ei) in this case can be expressed as
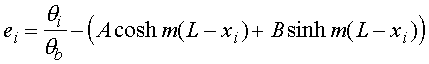
Then the sum of the squares of the residuals can be expressed as
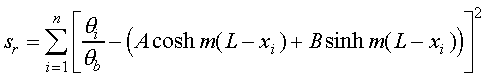
In order to determine values for A and B, the residual must be minimized.
Equation 16 is first differentiated with respect to each coefficient and
the results are then set equal to zero.
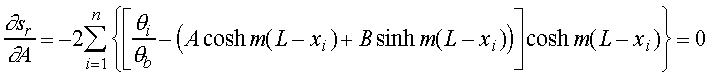
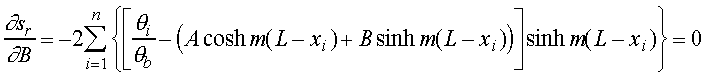
These equations represent a set of 2 equations with 2 unknowns, A and B.
The equations may be solved (with some difficulty) to give
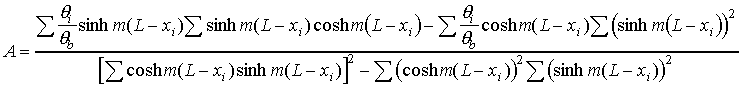
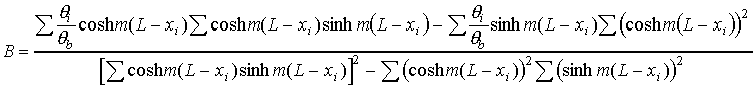
Note that the denominator is the same in each equation and that the summation
symbols have been simplified; all summations are from i = 1 to n. These equations
may be designated as equations 19 and 20. Only one problem remains; the solutions
for A and B are dependent upon the variable m, which contains the heat transfer
coefficient h (the desired solution)! This dilemma may be overcome by an
iterative procedure which will provide the best values of A, B, and h.
The best fit from the method of least squares may be provided by minimizing
the variance, a statistical parameter that indicates the spread of the data
about the curvefit line. The variance
(Syx2) for this equation form
is
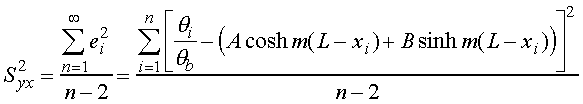
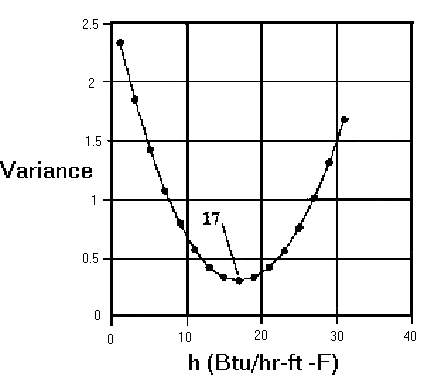
Two possibilities present themselves for completing the iteration process.
In order to find the minimum variance, the derivative of the variance with
respect to m must equal zero. This requirement must be met in order to complete
the iterative scheme. A second, less elegant solution method, involves the
determination of the variance for a number of assumed values of h. The variance
as a function of h is then plotted and the minimum inflection point on the
graph will indicate the value of h for the fin. Figure 3 is an example plot
of a possible functional relationship between the variance and h.
Objectives
This experiment was designed to demonstrate the concept of a fin as it relates
to the heat transfer field and to present a statistical method for the
determination of a physical parameter such as the heat transfer coefficient.
Experience will also be gained in modeling the physical situation, in the
acquisition of data that characterizes that physical situation (and the judicious
use of same), and in the study of a one-dimensional approximation.
Experimental Apparatus
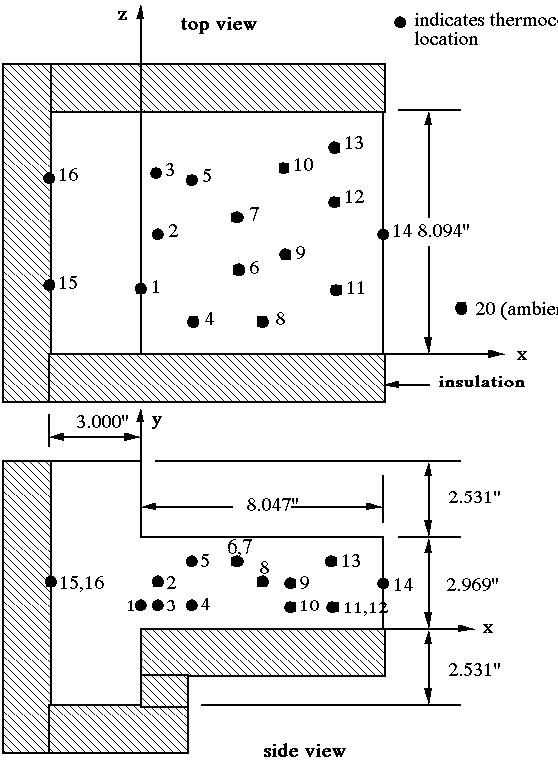
A model of a one-dimensional fin is provided for this experiment. Figure
4 details the fin dimensions and the approximate locations of the type K
thermocouples while Table 1 gives exact thermocouple locations within the
304 stainless steel. In the present configuration, the fin is insulated on
the bottom and sides with two inches of calcium silicate brick insulation.
Thus, from a thermal point of view, the design represents the upper half
of a symmetric, infinitely wide (in the z direction) fin.
Heat is supplied to the fin base by two Watlow strip heaters that are wired
in parallel to a power supply. The maximum design total heat input is 600
watts. The thermocouples are connected to a 20 channel selector which, in
turn, is connected to a digital readout.
Procedure
The apparatus will be turned on before class to ensure that a steady state
condition exists. Do not touch any of the stainless steel surfaces or adjust
the settings on the power supply.
Questions and Points of Interest
In the discussion of the results the following items should be considered
(as a minimum):
References