ME
354 - Thermofluids Laboratory
Spring 1997
LAB 6 - Flow Through a Circular Pipe
Introduction
In any viscous flow, the fluid in direct contact with a solid boundary
has the same velocity as the boundary itself and the "no-slip condition"
must be satisfied at the boundary. Since the fluid velocity at the stationary
solid surface is zero, but the bulk fluid is moving, velocity gradients
(and hence shear stress) must be present in the flow. For one-dimensional
viscous flow, the shear stress t is given by
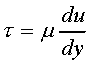 (1)
(1)
where 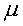 = dynamic viscosity, u = stream wise velocity,
and y = normal coordinate measured from the
solid boundary.
= dynamic viscosity, u = stream wise velocity,
and y = normal coordinate measured from the
solid boundary.
Thus, in pipe flow as shown in Figure 1, the wall shear stress can be determined
from knowledge of the velocity profile and by changing from a cartesian
to a cylindrical coordinate system.
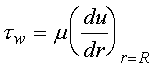 (2)
(2)
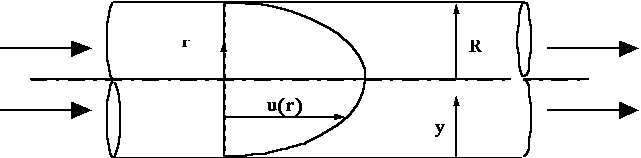
Figure 1. Circular Duct Nomenclature
For an internal flow in which the fluid is constrained by the bounding
walls, the viscous effects will grow and eventually meet at the tube centerline.
This occurs in the entrance region of the pipe where the nearly inviscid
freestream flow first enters the tube. Viscous boundary layers grow downstream,
slowing down the axial flow at the wall, and causing the center-core flow
to accelerate in order to maintain the principle of conservation of mass
for an incompressible fluid. The accepted correlation for the entrance
length, Le (from pipe entrance to point where fully
developed flow first occurs), in laminar flow is
Le/d 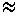 0.06 Red laminar (3)
0.06 Red laminar (3)
where d = pipe diameter. In turbulent flow, the boundary layers develop
faster and the accepted correlation for Le is
Le/d 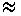 4.4 Red1/6
turbulent (4)
4.4 Red1/6
turbulent (4)
Following the entrance region, the flow becomes fully developed. The velocity
profile in a fully-developed laminar flow in a circular duct is well established
and is given by the parabolic equation
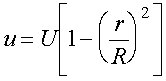 (5)
(5)
where U = the maximum velocity at a cross section of the duct, r
= the radial coordinate measured from the duct centerline, and R
= the duct radius.
Except for flows of very viscous fluids in small diameter ducts, most internal
flows are turbulent. In turbulent flow the relationship between the stress
field and the mean velocity is a bit more complicated. The accepted theory
on the velocity profile for turbulent flow considers three regions near
the wall. In the wall layer, viscous shear dominates. In the outer layer,
turbulent shear dominates, while in the overlap layer between the wall
layer and the outer layer, both types of shear dominate. In the wall layer,
the wall law for the velocity profile follows a linear viscous relationship
u+ = u/u* = yu*/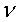 = y+ (6)
= y+ (6)
where u* = (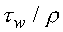 )1/2,
and
)1/2,
and 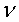 =
kinematic viscosity.
=
kinematic viscosity.
This inner-wall law usually covers less than 2% of the total profile and
can be neglected in most cases. The overlap layer velocity can be shown
to vary logarithmically with y
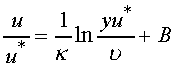 (7)
(7)
The constants in this equation are best approximated by 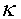 = 0.41 and B = 5.0. Since the inner wall law can be neglected and
the outer law profile is close to that of the overlap layer, equation 7,
the logarithmic overlap law, approximates the entire velocity profile quite
well for pipe flow. The value of u* can be determined by evaluating
eq. 7 at the centerline. Here, y = R, u = u0
and eq. 7 becomes
= 0.41 and B = 5.0. Since the inner wall law can be neglected and
the outer law profile is close to that of the overlap layer, equation 7,
the logarithmic overlap law, approximates the entire velocity profile quite
well for pipe flow. The value of u* can be determined by evaluating
eq. 7 at the centerline. Here, y = R, u = u0
and eq. 7 becomes
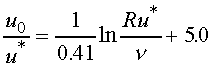 (8)
(8)
The average velocity V can be found by integrating the velocity profile
u (determined either experimentally or theoretically)
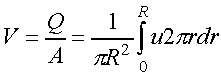 (9)
(9)
Using the theoretical velocity profile from eq. 7, where y = R
- r, the integration will yield
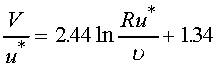 (10)
(10)
Further, it can be shown that V/u* is directly related to the Darcy
friction factor according to the following relationship
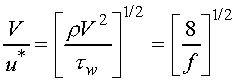 (11)
(11)
The logarithm argument in equation 10 is equal to
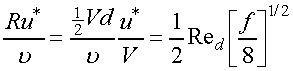 (12)
(12)
Substituting eq. 11 and 12 into eq. 10, changing to a base-10 logarithm,
adjusting the constants to fit the experimental data better, and rearranging,
results in the accepted formula for the relationship between Re and f for
smooth-walled pipes
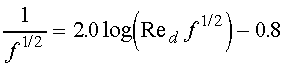 (13)
(13)
Experimental Apparatus
A long circular PVC pipe (I.D. = 2.041 in) with a square-edged entrance
has been instrumented for this experiment. Room air can be induced into
the tube by a centrifugal fan and the flow rate may be controlled with
a globe valve. A pitot tube is mounted in the test section (clear pipe,
I.D. = 2.047 in) at a distance 3.20 m from the tube entrance. The pitot
tube can be moved in the radial direction inside the pipe using a traversing
mechanism that is scaled in 0.001" increments (1 revolution = 0.025
in). Both the static and stagnation pressure taps on the pitot tube are
connected to a manometer in order that the difference between these two
pressures may be measured directly. Other instrumentation includes a type-K
thermocouple inserted into the flow stream near the tube exit, a manometer
to indicate the static pressure at the pitot tube, and an orifice meter
(orifice diameter = 1.5 in) which can be used to determine the volumetric
flow rate. The air velocity can be determined from the pressure difference
data and the air density. The wall shear stress, friction factor, average
velocity, and flow rate can be calculated from the velocity profile.
Pitot Tube
If Red > 1000, where d is the probe diameter, the
flow around the probe is nearly frictionless and Bernoulli's equation applies
with good accuracy. For incompressible flow, and neglecting any elevation
head, the following expression relates the local velocity to the difference
in stagnation and static pressure:
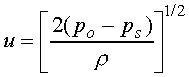 (14)
(14)
where po = stagnation pressure, ps
= static pressure, and 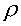 = fluid density.
= fluid density.
The difference between the stagnation and the static pressure can be measured
in terms of h inches of water so that equation 14 can be rewritten as
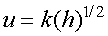 (15)
(15)
where k is a constant.
Orifice Meters
The orifice meter is one of a general category of restrictive type fixed
area meters. The flow-related signal is a pressure difference, measured
between the two points on the meter body as shown in Figure 2. These meters
accelerate the fluid stream by imposing a contraction on the flow area,
and then decelerate the flow, by expanding back to the original pipe diameter.
As the fluid accelerates, its static pressure is reduced. As the fluid
decelerates, the pressure rises again, but not without loss. Losses are
related to irreversibilities in the flow field; eddy structures and turbulence.
Mechanical energy dissipated by these mechanisms must be provided by flow
work done by the main stream. The result is a loss of pressure. Expressions
for mass flow rate and for volumetric flow rate Q can be obtained from
the energy equation and the continuity equation. The volumetric flow rate
in terms of the pressure drop (p1
- p2) between the 2 pressure taps
is
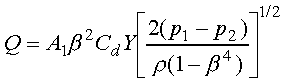 (16)
(16)
where A1 = 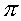 D12/4
(pipe cross-sectional area),
D12/4
(pipe cross-sectional area), 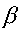 = d/D1 (ratio of orifice to pipe
diameter), Cd = discharge coefficient,
and Y = compressibility factor. The discharge coefficient is a function
of the Reynolds number and the diameter ratio and is the ratio of actual
discharge to the theoretical discharge.
= d/D1 (ratio of orifice to pipe
diameter), Cd = discharge coefficient,
and Y = compressibility factor. The discharge coefficient is a function
of the Reynolds number and the diameter ratio and is the ratio of actual
discharge to the theoretical discharge.
For thin plate orifice meters, 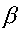 should be in the range of 0.2 to 0.8, except that the hole should not be
less than 12.5 mm. Three types of tappings are commonly used to obtain
the pressure drop across the obstruction. The most common of these tappings
are D and D/2 taps in which the taps are located 1 diameter upstream and
1/2 diameter downstream of the orifice plate. For a square-edge orifice
meter with D and D/2 taps, ASME [2] recommends the following curve-fit
formula for determining the discharge coefficient
should be in the range of 0.2 to 0.8, except that the hole should not be
less than 12.5 mm. Three types of tappings are commonly used to obtain
the pressure drop across the obstruction. The most common of these tappings
are D and D/2 taps in which the taps are located 1 diameter upstream and
1/2 diameter downstream of the orifice plate. For a square-edge orifice
meter with D and D/2 taps, ASME [2] recommends the following curve-fit
formula for determining the discharge coefficient
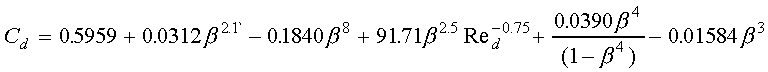 (17)
(17)
where Red = Reynolds number based on pipe diameter.
The actual calculation of Cd is iterative since
Cd is a function of Reynolds number, which
itself is a function of the flow rate (what you are looking for in the
first place!). To begin the iteration, guess a value for Red,
calculate Cd, evaluate the actual flow rate,
determine a new value of Red and compare to the initial
guess for Red. If these values differ, use the new
value of Red and repeat the calculations until the
new and old values of Red are acceptably close. This
process usually requires only 2 or 3 iterations.
When flow measurements of incompressible fluids are made, the expansion
factor Y equals unity. For compressible fluids flowing through a
square-edge orifice with D and D/2 taps, an empirical expression for Y
is given as [3]
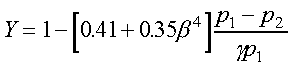 (18)
(18)
where 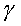 is the specific heat ratio (
is the specific heat ratio (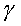 =
1.4 for air). For a given pressure drop across the restriction, Y
is constant and thus does not change during the iterative calculation process
used to calculate the actual flow rate (only Cd
is a function of flow rate).
=
1.4 for air). For a given pressure drop across the restriction, Y
is constant and thus does not change during the iterative calculation process
used to calculate the actual flow rate (only Cd
is a function of flow rate).
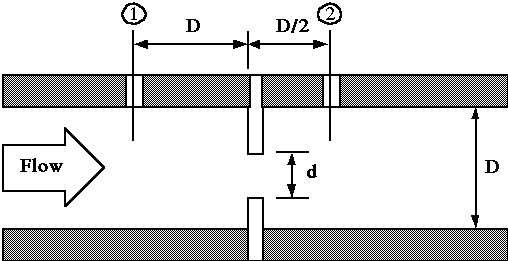 Figure 2. Orifice Meter With D and D/2 Taps
Figure 2. Orifice Meter With D and D/2 Taps
Manometer Fluid
The fluid in all of the manometers is Meriam D-2673 Red Oil. The specific
gravity of the red oil is temperature dependent and is given as
SG = 0.8497 - 0.00038T
where T = red oil temperature (°F).
The red oil specific gravity is referenced to the density of water at 4°C
(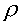 = 62.422 lbm/ft3).
= 62.422 lbm/ft3).
Objectives
-
To measure and plot the velocity profile.
-
To calculate the flow rate from the velocity profile and from an orifice
meter.
-
To calculate the wall shear stress, Darcy friction factor, and average
velocity.
Procedure
-
Determine the room temperature, barometric pressure and the radius
of both pipe sections.
-
Set the pitot tube at a reference position.
-
Start the fan and set the control valve to obtain the desired speed.
-
Move the pitot tube at suitable intervals and note the pressure difference
(po - ps) in the manometer at
each interval. Also record the static pressure and the temperature of the
air stream.
-
Record the pressure drop across the orifice meter.
-
Calculate the velocity at different radii and plot the velocity profile.
Compare this velocity profile to the expected velocity profile predicted
by theory. Is this profile symmetrical considering the uncertainty of the
measurements?
-
Calculate the average velocity V from the experimental velocity profile
and from theory. If the flow is laminar, compare the radial location at
which the average velocity equals the actual air velocity. How does this
compare to the predicted value? Compare and discuss the values of V obtained
from the orifice meter and the two previously mentioned methods.
-
Verify the volume flow rate obtained by integrating the experimental
velocity profile with that obtained with the orifice meter. Discuss any
contributing factors that would cause a discrepancy between the values
of volume flow rate obtained by the two methods.
-
Determine the wall shear stress using the definition of viscosity and
from the definition of u*. Discuss any differences.
-
Compute the Darcy friction factor and compare to the value predicted
from the Moody diagram or from the either the Colebrook or Haaland equations
(eqs. 6.64 and 6.64a in White, Fluid Mechanics).
References
-
White, F.M., Fluid Mechanics, 3rd Ed., McGraw-Hill Book Co., New York,
1994.
-
ASME Fluid Meters Research Committee, The ISO-ASME Orifice Coefficient
Equation, Mechanical Engineering, pp. 44-45, July 1981.
-
Holman, J.P., Experimental Methods for Engineers, 4th Ed., McGraw-Hill
Book Co., New York, 1984.

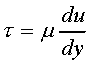 (1)
(1)
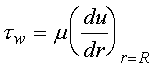 (2)
(2)

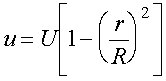 (5)
(5)
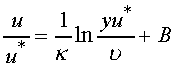 (7)
(7)
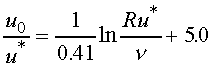 (8)
(8)
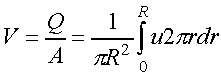 (9)
(9)
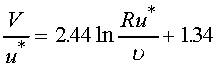 (10)
(10)
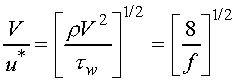 (11)
(11)
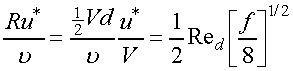 (12)
(12)
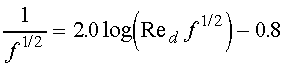 (13)
(13)
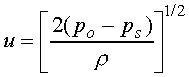 (14)
(14)
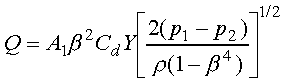 (16)
(16)
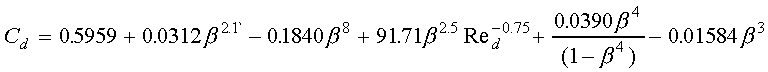 (17)
(17)
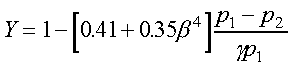 (18)
(18)
